「数学の授業で『球の体積と表面積の公式、覚えておくように!』と言われたけれど、いまいちピンとこない…。」そんなふうに感じていませんか?公式をただ暗記するのは大変ですが、意味が分かればぐっと覚えやすくなります。この記事では、球の体積・表面積の公式の覚え方や、忘れてしまったときの考え方を分かりやすく解説していきます。
球とは
皆さんは「球」と聞いて何をイメージするでしょうか?日常生活ではサッカーボールなど、丸いボールをイメージすると思います。サッカーのことを蹴球と言ったり、バレーボールを排球と言ったりもしますね。

数学においての定義では、球は「空間において、ある点から等距離にある点の集まり」です。似たような定義として円(「平面において、ある点から等距離にある点の集まり」)がありますので、こちらも合わせて覚えておきましょう。球と円の違いは、考えている範囲が空間か平面か、の違いになります。
球の体積の求め方
公式と覚え方
半径がrの球の体積Vは(円周率πを用いて)

この公式を覚える際には、rの次数に注意しましょう。球が立体、すなわち3次元であることから、単位を考えると3乗になります。というのも、皆さんが体積の単位は?と聞かれて思い浮かぶ単位に、m3(立方メートル)やcm3(立方センチメートル)があると思います。また、身近な公式では一辺がrの立方体の体積はr3と表しますね。これらを見てお分かりいただけるように、体積の単位は長さの3乗で表します。
例題
半径が3の球の体積Vは?

<別解>公式を思い出せない時はコレ
球の体積は、半径が同じ円柱の体積から導くことができます。なぜなら、半径が同じ円柱と球の体積比は3:2になるからです。
下の図をご覧ください。円柱と球、それぞれの体積を計算することにより、体積比 円柱:球=3:2が導けます。

球の公式を忘れてしまった…!そんなときでも円柱の体積を2/3にすれば球の体積になることを覚えていれば、自分で球の体積を導くことができます。
球の表面積の求め方
公式と覚え方
半径がrの球の表面積Sは

球の表面積の覚え方は、体積と同じように、面積の単位がm2(平方メートル)やcm2(平方センチメートル)と表すことから、rの次数は2であることが分かります。
例題
半径が4の球の表面積Sは?

球の体積・表面積の間違えやすい問題にチャレンジ
まずはウォームアップの問題から!
問題1(正答率:36%)

まずは、自分で考えてみましょう。困ったら下のヒントを見てみてください。自力で解答まで出せそうな人は是非ヒントを見ずに解ききってくださいね!

【正解】
体積をV、表面積をSとすると、
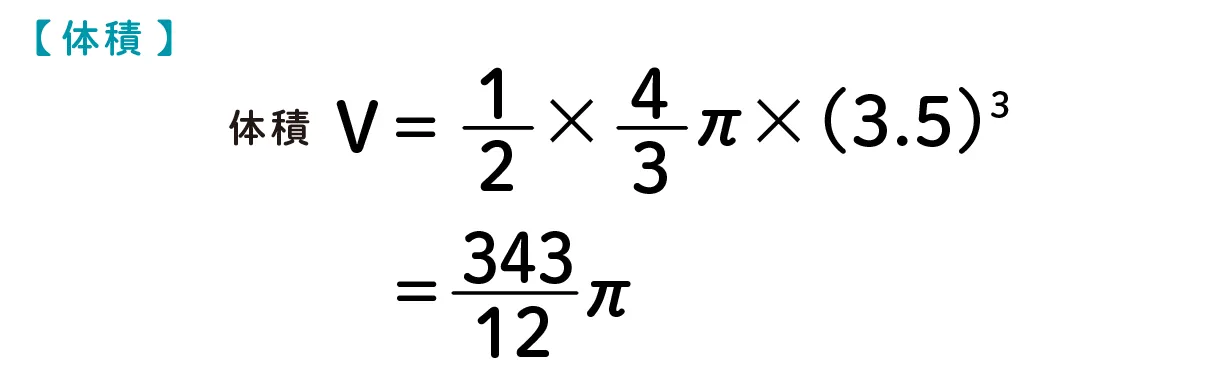

今度はさらに難しい問題に挑戦!
問題2(正答率:33%)


【正解】
直線lを回転の軸として1回転させると、下の図のような球になるので、



<解き方の解説>
図形を回転させる問題はこのように考えよう
回転後の立体をいきなりイメージするのは難しいため、複雑な図形にも対応できる方法をご紹介します。
ポイントは、ずばり3つ。
- 図形上で一点を決めて、軸のちょうど反対側に点を描く
- それを何回か繰り返す
- 元の点と軸の反対側の点を繋ぐと回転した図形になる

点が回転し動いた跡は円になります。この方法を使えば、下のような図形も1回転させた図を描くことができます。下に練習問題としてまた別の図形を回転させた後の立体を載せています。

【高校生向け】なぜこの公式になるのか?
実は、微分・積分を駆使すると体積・表面積の公式を証明することができます。それぞれ5分あればしっかり目を通せる内容になっているので、気になった方は是非読んでみてくださいね。ではまず体積から見てみましょう。
球の体積の場合
まず、球を円が幾つも積み重なってできた立体と見てみましょう。ここではx軸に垂直な面で球を輪切りにして考えます。

具体的には、この球を極限まで薄い輪切りにしていったとき、最終的には限りなく薄い円柱が積み重なった状態、と考えることができます。これを積分していくことで球の体積を求めていきましょう。
この限りなく薄い円柱は、「半径が\(\sqrt{r^2 - x^2}\)の円を底面とした、高さ\(dx\)の円柱」となるので、この微小円柱の体積は、
\(\pi \times \left( \sqrt{r^2 - x^2} \right)^2 \times dx = \pi (r^2 - x^2) \,dx\)
です。
ゆえに、これを\(-r \leqq x \leqq r\)の範囲で積分すると、
\(\int_{-r}^{r} (r^2 - x^2)\pi\,dx = \frac{4}{3} \pi r^3\)
となり、球の体積の公式が証明されます。
球の表面積の場合
次に、表面積です。ここでは表面積は2つの証明の方法をご紹介します。
ではまず1つ目、球の体積の公式を利用する方法です。限りなく薄い膜が重なって球ができていると考えます。すると膜を一枚ずつ剝がしていったとき、最終的には幾つもの薄い膜が球を形作っているので、球の体積とはこの薄い膜の体積の和を足したものになります。球の中心からの距離をtとすると、球の表面積を0≦t≦rで積分すると球の体積になるということですね。球の形をしたマトリョーシカをイメージしてください。

はじめに、先ほど証明した球の体積(\(V = \frac{4}{3} \pi r^3\) )とこの考え方を合体させると、
\(\int_0^r S(t)\,dt = \frac{4}{3} \pi r^3\)
が成り立ちますね。
これを両辺rで微分すると、
表面積 \(\ S(r) = 4\pi r^2\)
となり、球の表面積が求まります。
次に2つ目の方法です。今度は球を輪切りする方法で考えてみましょう。

中心からの角度が \(\theta\) から \(\theta + \Delta\theta\) の部分の表面積を考えます。
これは、\(\Delta\theta\) が限りなく0に近いとき、赤い部分の面積は 図のように、\(r \Delta\theta \times 2\pi r \cos\theta\) となります。
よって、これを \(\theta\) の値が \(-\frac{\pi}{2}\) から \(\frac{\pi}{2}\) まで足し合わせると、
\(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} 2\pi r^2 \cos\theta \, d\theta = 4\pi r^2\)
となり、同じく球の表面積が求まります。
球の表面積を積分すると球の体積になる。言い換えると球の体積をr(半径)で微分すると球の表面積になる。このことは球の公式を覚える手助けにもなるので、ぜひ知っておいてください。
まとめ
球にまつわる重要な公式について解説しました。
公式は、使っていくうちにだんだんと身についていくものです。「初めは公式を見ながら解く」「慣れてきたら何も見ずに解いてみる」のように、実践を通して少しずつ身につけていくことが数学で点を取るための秘訣です。たくさん演習を積んで、公式をマスターしてくださいね。
atama+塾・atama+ オンライン塾では、AI教材「atama+」を使って、数学の力を効率的に身につけることができます。詳しい情報や無料体験をご希望の方は、以下のリンクからお問い合わせください。
{{Posts-CTA}}


.svg)

.svg)